재료 데이터베이스와 인공지능 융합을 통한 복합재료 특성 분석
Identifying unknown material properties using reverse engineering by combining materials databases and artificial intelligence
Koji Yamamoto | CYBERNET SYSTEMS CO.,LTD.
■ Abstract
이번 연구에서는 가상 재료 시험(virtual material testing)을 활용하여 복합재료(FRP)의 정적 강도를 정밀하게 예측하는 방법을 제시하였다. 민감도 분석 결과, 복합재료의 강도는 섬유-수지 계면 특성과 수지의 탄성계수, 포아송비에 크게 의존함을 확인하였다. 이러한 결과를 바탕으로 가상 시험과 실제 재료 시험 데이터를 결합하고, AI 학습을 통해 복합재료의 재료 상수를 역식별하였다. 학습된 AI는 실제 시험 결과와 잘 일치하는 재료 상수 및 응력-변형 곡선을 제시하였으며, 섬유 방향에 따른 파괴 거동도 성공적으로 재현하였다. 이를 통해 가상 재료 시험의 유용성과 AI 기반 분석 적용 가능성을 확인할 수 있었다. 더 나아가 향후에는 탄소성 및 점탄성과 같은 비선형 거동뿐만 아니라 FRP 외의 다양한 미세구조 재료 특성 예측에도 활용 가능할 것으로 기대된다.
Introduction
Material constants are one of the most important factors for determining the accuracy of analysis results and are essential for designers to make confident material decisions. For materials with non-uniform microstructures, such as fibre-reinforced composites, failure is initiated by many factors. Typical examples are delamination between layers, fibres, and matrices; fibre breakage; and crack initiation and propagation within the resin. Unfortunately, it is usually very difficult to measure these properties directly by physical testing because the fractures often occur at the microscale level. Delamination strength can be measured by double cantilever beam testing or end-notch bending beam testing. This is the largest scale problem and is easy to characterize directly by experiment.
But what about failure modes between the fibre and the matrix?
One way to resolve this is through pull-out testing. This involves using a robotic arm to pull out a single fibre embedded in a droplet of resin. However, there are two problems with this test: one is that tangential stresses dominate at material interfaces and so the normal strength cannot be measured; the other problem is that the resin used in the experiment has a different moulding history to the actual FRP (fibre-reinforced plastic). There is no guarantee that the interfacial strength obtained in the tests can be directly applied to FRP problems. To accurately determine the information about the internal microstructure, it is important to use the actual FRP as the test specimen. Therefore, in this paper, in order to establish a highly accurate method of predicting the static strength of FRP, we first studied the factors that strongly influence the strength through sensitivity analysis. In addition, we present an example of the inverse identification of those factors (i.e. material constants) by reverse engineering methods that combine big data and artificial intelligence (AI). Both analyses require the preparation of large amounts of data on material behaviour under various test conditions. This data was obtained by testing virtual materials using the Ansys Multiscale.Sim add-on tool [1]. Note that the examples presented in this article are synopses of articles co-authored with collaborators. See references [2] and [3] for the detailed analytical methods and a description of the results.
■ Sensitivity assessment of the strength of composite materials
There are many factors that affect the strength of composite materials, but the degree of influence varies from factor to factor. Prior to the inverse identification analysis, the sensitivity of each factor to strength is evaluated by virtual materials testing. A surrogate model with a response surface was constructed from the analysis results for various sample conditions. Monte Carlo simulations were used to predict response to various macro rigidities and static strengths, which were then extracted from the data to identify key variables affecting static strength.
Fig. 1 and Table 1 provide an overview of the microstructural models and parameters with quantified material properties and variability, respectively. A surrogate model was created based on the results of the sample analysis conducted using partial factorial design with the L36 orthogonal array. The sensitivity of the analytical results was studied by applying the variability shown in Table 1 to the surrogate model.
<Fig. 1. FE (finite element) model of RVE (representative volume element) with random fibre distributions.>
[Table 1. Statistics of variation factors]
|
Variation factors
|
Shape
|
Mean
|
Standard deviation
|
|
Young’s modulus of resin [MPa]
|
Normal dist.
|
4207.8
|
404.7
|
|
Poisson’s ratio of resin [-]
|
Normal dist.
|
0.38
|
0.013
|
|
Volume fraction of fibre [%]
|
Normal dist.
|
56.3
|
1.74
|
|
Variation factors
|
Shape
|
Mean
|
Shape parameter
|
|
Strength of resin [MPa]
|
Weibull dist.
|
55.7
|
16.6
|
|
Strength of material interface [MPa]
|
Weibull dist.
|
95.7
|
9.0
|
<Fig. 2. Self-Organizing maps of variation indices of Monte Carlo simulation results.>
As shown in Fig. 2, we created a self-organizing map (SOM) to visualize the relationship between the large number of inputs and outputs in two dimensions. These results confirm that the Young's modulus and the Poisson's ratio of the resin, and the variations in fibre and resign strength correlate with changes in macro strength, and less so with fibre volumetric content and resin strength.
■ Identifying material properties for strength in microstructures
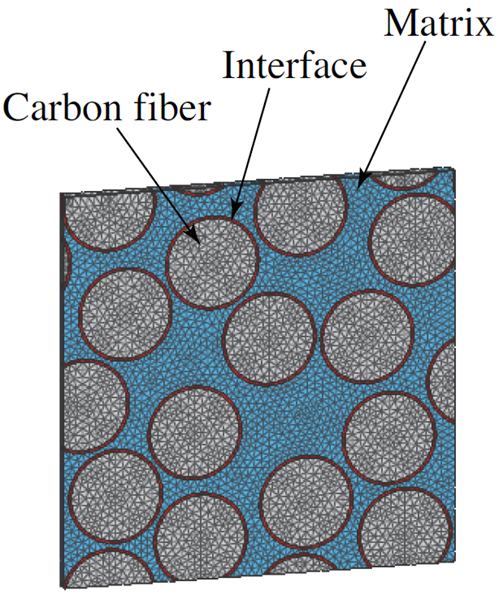
The SOM analysis showed that accurate input regarding interfacial strength is critical for predicting the static strength of composite materials. Although there are many models to describe interfacial delamination, in this study we used a type of bilinear approximation of the Cohesive Zone Model (CZM), as shown in Fig. 2. For each of the two modes in which delamination occurs, the contact stiffness increases as the distance between the contact surfaces and the amount of slip increases. There are four material constants: the threshold for the onset of delamination at the material interface and the amount of space in which contact stiffness completely disappears for the two delamination modes.
<Fig. 3. Concept of the bi-linear approximation of the cohesive zone model.>
As shown in Fig. 3, we propose a combination of experimental and analytical approaches to identify these material constants. The analysis consists of three phases. The first is a learning phase for the AI in which a large set of input parameters related to the unknowns of the microstructure, and the output parameters representing the response of the macroscopic materials are generated by virtual material tests. Here, the unknown quantities are the fibre volume content, the matrix strength, and the interface strength. In addition, tests on real materials are also performed under the same conditions as the virtual material tests. This undoubtedly reveals the true essence of the real FRP material. Therefore, in the second phase, the test results of the real materials are transmitted to the output of a well-trained AI and unknown input parameters are proposed to obtain the output. Finally, the virtual material is tested again using the properties identified. This is compared with the results of the real material tests to validate the series of analytical approaches.
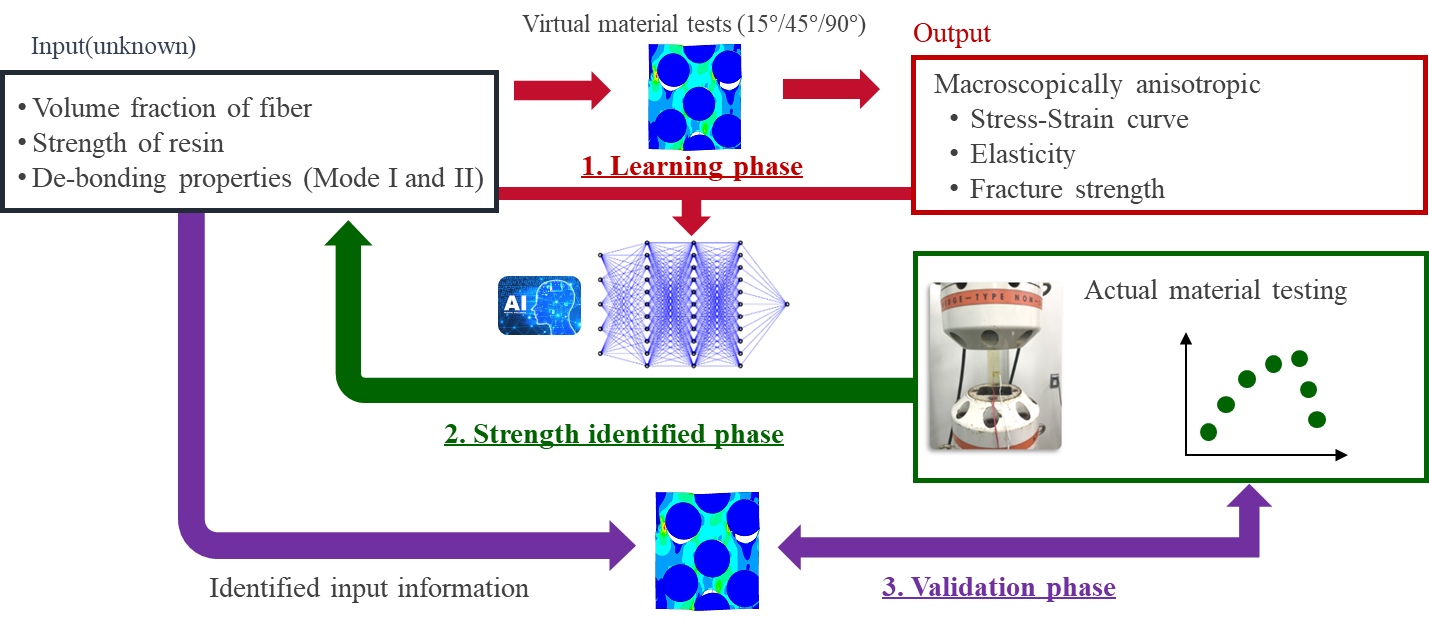
<Fig. 4. Workflow to identify material constants by inverse analysis.>
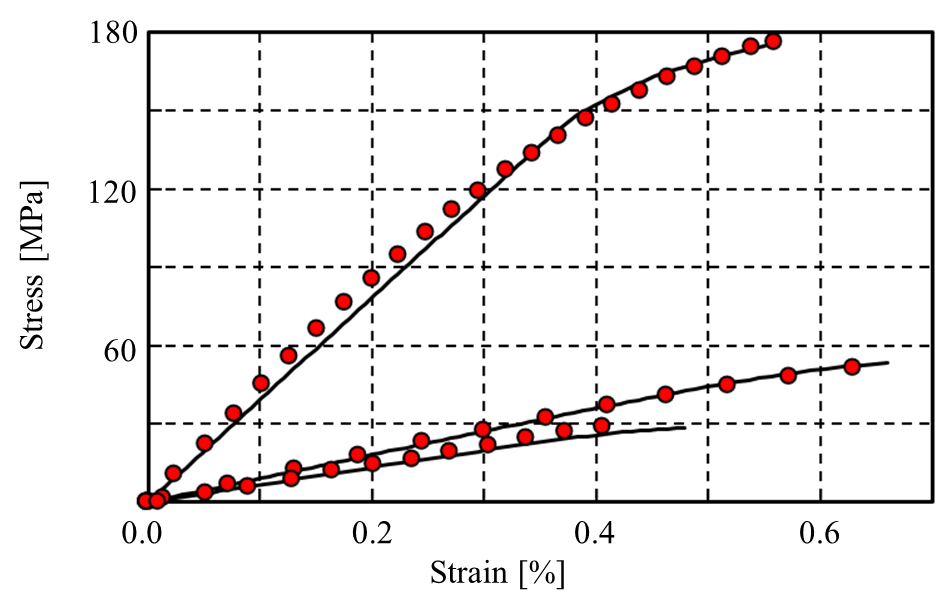
The identified material constants and the stress-strain curves obtained consequently are shown in Table 2 and Fig. 5. Young's modulus and the fracture strength properties of the FRP are also shown in Table 3. To measure the influence of the two modes of interfacial delamination, material tests were conducted off-axis with the fibre orientation tilted away from the loading direction. As the fibre orientation approaches an angle parallel to the loading axis, interfacial de-bonding due to the tangential component dominates (the only exception is at 0°C where fracture due to fibre breakage dominates). The analysis reproduces the experimental results well for all test orientations.
<Fig. 5. Stress-strain curve obtained from virtual material testing using material constants identified.>
[Table 2. Material constants identified]
|
Parameter
|
Output by inverse analysis
|
|
Strength of matrix
|
90.8 [MPa]
|
|
De-bonding threshold (Normal dir.)
|
63.4[MPa]
|
|
De-bonding threshold (Tangential dir.)
|
72.1[MPa]
|
[Table 3. Comparison of experimental and analytical intensities]
|
|
□ =15o
|
□ =45o
|
□ =90o
|
|
|
Ec [GPa]
|
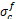 [MPa] [MPa]
|
Ec [GPa]
|
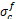 [MPa] [MPa]
|
Ec [GPa]
|
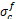 [MPa] [MPa]
|
|
Actual tests
|
44.2
|
176.5
|
9.44
|
51.7
|
7.33
|
29.9
|
|
Virtual tests
|
39.2
|
174.8
|
9.10
|
53.2
|
6.67
|
28.3
|
|
Error [%]
|
11.3
|
0.963
|
3.60
|
2.90
|
0.00
|
5.35
|
(□ : fibre orientation, Ec: Young’s modulus as composites, 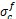 : Strength as composites)
: Strength as composites)
Conclusion
In this article, two analyses were performed to establish a highly accurate method for predicting the static strength of composite materials using virtual material testing, and the results are presented.
- Virtual material tests were conducted using various material parameters related to microstructure to quantify the factors affecting the strength of composite materials. SOM analyses show that the strength of composites containing unidirectional reinforcement is relatively strongly affected by the strength of the material interface and the Young's modulus and Poisson's ratio of the resin.
- A large amount of material test data was used to train the AI to identify those factors through inverse analysis. The results agreed well with the measured values.
Virtual material testing is very useful for generating the large amount of material test data required for inverse identification analysis. Not only can the tests be done in a short time, but they are also easy to conduct under any conditions. The diversity of input conditions increases the generalizability of the AI. In the present analysis, the matrix was assumed to have elastic properties, but in principle, non-linearities such as elasto-plasticity and viscoelasticity can be accommodated. Moreover, since microstructure is not limited to FRP, it is possible to predict the material properties of various microstructures that are difficult to measure in practice.
■ References
- [1] https://www.cybernet.co.jp/ansys/product/lineup/multiscale/en/multiscale/
- [2] Y. Ishibashi et al, “Suppression method of static strength variations of CFRP with data mining techniques”, (Japanese), 23rd proceedings of Japan Society for Computational Engineering and Science, 2018
- [3] R. Takami et al, “Evaluation of Interface Adhesion Strength of Unidirectional CFRP using Numerical Material Test and Neural Network”, (Japanese), Japan Society for Composite Materials, Vol. 48, 2022
■ About CYBERNET
CYBERNET is a leading digital engineering solutions company established in 1985 and headquartered in Tokyo, Japan. Its corporate slogan is "Making the world more convenient and richer through the unlimited possibilities of people and advanced technology." CYBERNET is an Apex Channel Partner and a Technology Partner of Ansys. The company has been developing Multiscale.Sim since 2007, and it is used by many customers in Japan and around the world.


![]() : Strength as composites)
: Strength as composites)



![[구조해석] Multiscale analysis System 소개](/image/thumb_document_blue.jpg)
![[열린세미나] 복합재료의 섬유 방향별 재료 특성을 고려한 구조해석 방법(Multiscale.sim)(14:00~14:40)](/storage/upload/data/thumbnail/1702798572_dXbubLB9d7OPl63wQsZ3lJ6mrCDQjxxEKA5tVKFc.png)



 ㈜태성에스엔이
㈜태성에스엔이