ANZINE : CAE 기술 매거진
이전 ANZINE Home Tech-Insight
축대칭 구조 해석의 새로운 접근 General Axisymmetric 요소 활용하기
- 장형진 수석매니저
- 태성에스엔이
- hjjang@tsne.co.kr
축대칭 구조 해석의 새로운 접근 General Axisymmetric 요소 활용하기
Introduction
축대칭 구조물은 회전체, 압력용기, 실링, 파이프 등 다양한 산업에서 널리 사용된다. 이러한 구조는 단면 형상이 축을 기준으로 회전해 만들어지기 때문에 일반적으로 2차원 축대칭 해석 기법이 활용된다. 하지만 기존 축대칭 해석은 기하학과 하중이 모두 축대칭이어야 한다는 전제가 필요해, 실제 현장에서 자주 발생하는 부분 하중, 편심 조건, 국부 접촉, 체결 불균일과 같은 비대칭 거동을 반영하기 어렵다는 한계가 있다. 이러한 경우 전체 3차원 모델을 구성해야 하며, 이는 모델링과 해석 시간 증가로 이어진다. Ansys에서 제공하는 General Axisymmetric 요소는 이러한 제약을 보완하기 위해 도입된 기법이다. 축대칭 단면을 기반으로 하면서도 하중과 변위를 Fourier Series로 표현하여 비대칭 거동까지 모델링할 수 있다. 본 고에서는 General Axisymmetric 요소의 개념과 특징을 소개하고, 기존 축대칭 해석과 비교하여 이 기법이 제공하는 새로운 접근법을 살펴보고자 한다.
■ General Axisymmetric 요소란?
General Axisymmetric 요소는 축대칭 단면을 기반으로 하되, 구조의 비대칭 거동까지 표현할 수 있도록 확장된 요소이다. 기존 축대칭 요소가 θ 방향(원주 방향) 변화를 고려하지 못했던 것과 달리, 변위를 Fourier Series 형태로 표현하여 θ 방향의 변형 및 하중 변화를 함께 모델링한다. 이를 통해 2차원 단면 모델임에도 불구하고 실제 3차원 구조에서 나타나는 편심 하중, 국부 하중, 비대칭 접촉, 체결 불균일 등 다양한 비대칭 현상을 효과적으로 재현할 수 있다. [그림 1]은 General Axisymmetric 요소의 기본 형상을 나타낸 것으로, 축대칭 단면(Base Element)이 θ 방향으로 여러 개의 Nodal Plane으로 확장되며 전체 3차원 거동을 구성하는 개념을 보여준다.
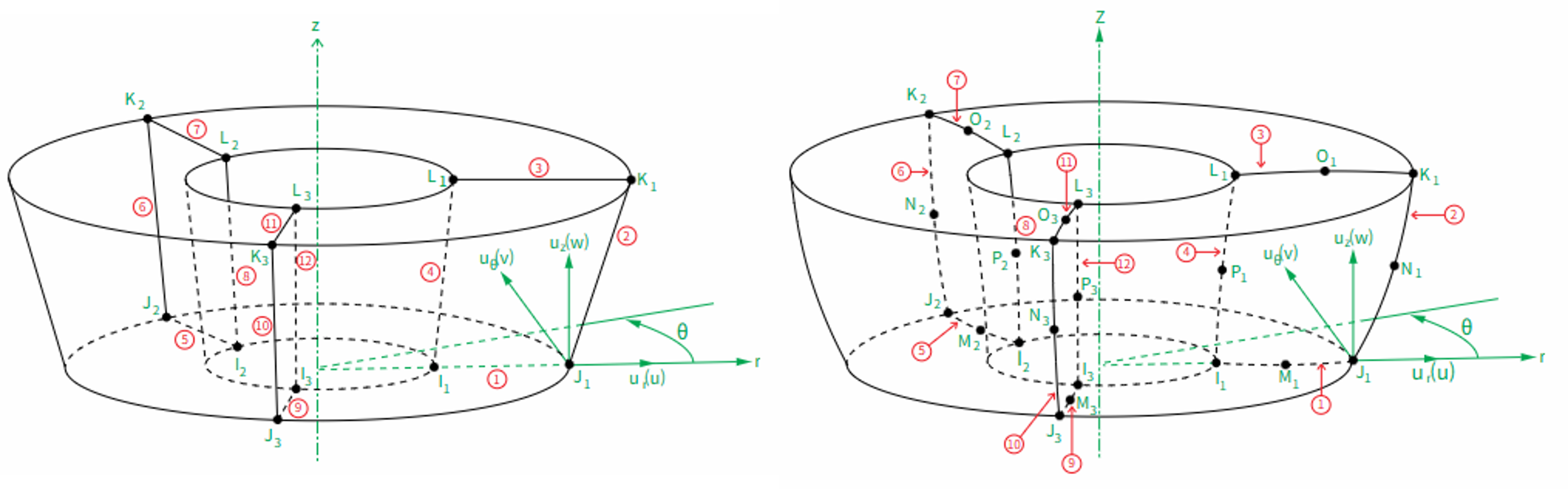
[그림 1] SOLID272, SOLID273 요소 형상
General Axisymmetric 요소는 다음과 같은 특징을 가진다.
- SOLID272 / SOLID273 요소 기반
- 기하학은 2D 축대칭이지만 거동은 3D를 반영
- 하중·변위의 θ 방향 변화를 모드(Mode)로 정의하여 해석
- 선형/비선형 해석 모두 지원
- Modal, Static, Harmonic, Transient 등 대부분의 해석 유형에 적용 가능
요약하면, General Axisymmetric은 2D 축대칭 모델의 효율성과 3D 모델의 정확성을 동시에 확보할 수 있는 요소 기술로서 기존 축대칭 해석의 한계를 크게 확장해준다.
■ General Axisymmetric 설정 방법
General Axisymmetric 해석을 수행하기 위해서는 먼저 축대칭 단면을 정의해야 한다. 본 예제에서는 [그림 2]와 같이 중공형 실린더 단면을 모델링하였다. 이 단면은 실제 3차원 구조를 θ 방향으로 확장하는 데 사용되는 기본 Base Element 역할을 한다.
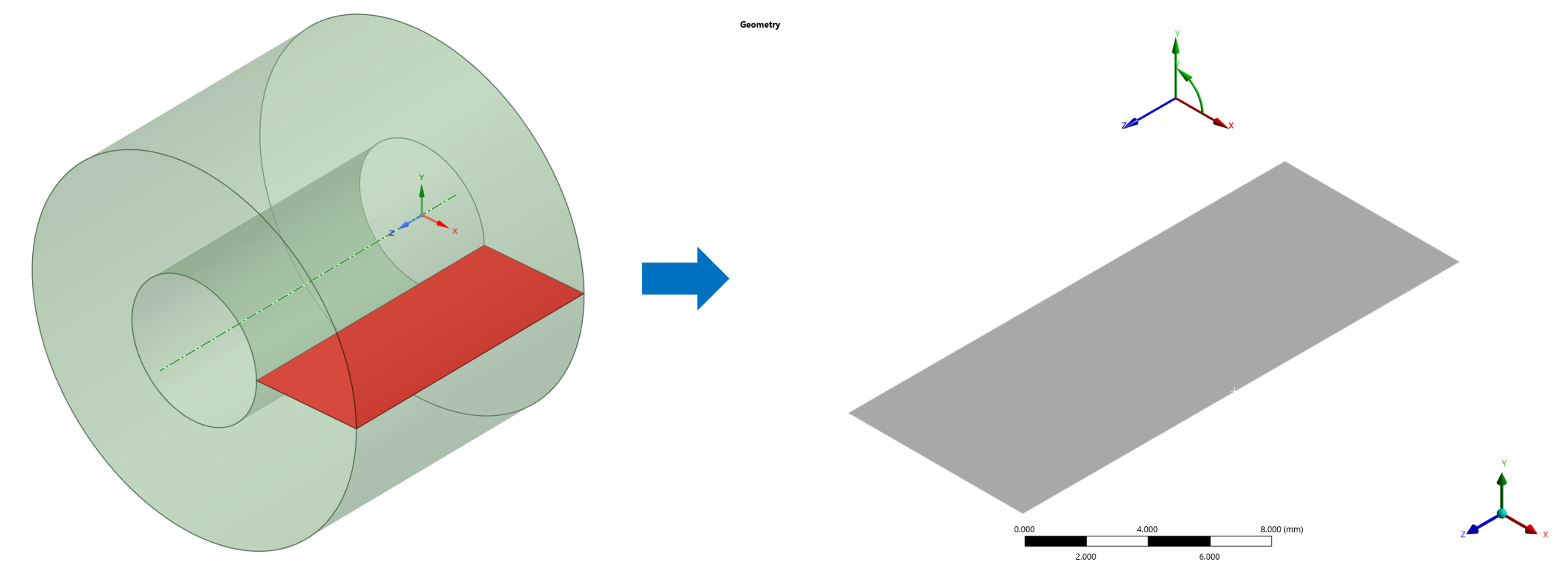
[그림 2] 축대칭 형상
[그림 3]은 Ansys Mechanical에서 General Axisymmetric 기능을 활성화한 화면으로, 축대칭 단면이 θ 방향으로 확장되며 Nodal Plane이 생성되는 구조를 보여준다. Symmetry 탭에서 General Axisymmetric을 선택하면 해당 기능이 적용되며, Details 창에서 회전축 정의, 좌표계 지정, Nodal Plane 수 등을 설정하여 3차원 거동을 구성할 수 있다. Nodal Plane 수는 단면(Base Element)을 θ 방향으로 복제하는 개수이며, 이는 해석에 포함되는 모드 수와 직접적으로 연관된다. Nodal Plane 수가 많을수록 더 높은 차수의 비대칭 변형을 표현할 수 있으며, 현재 Ansys에서는 최대 12개까지 지원된다.
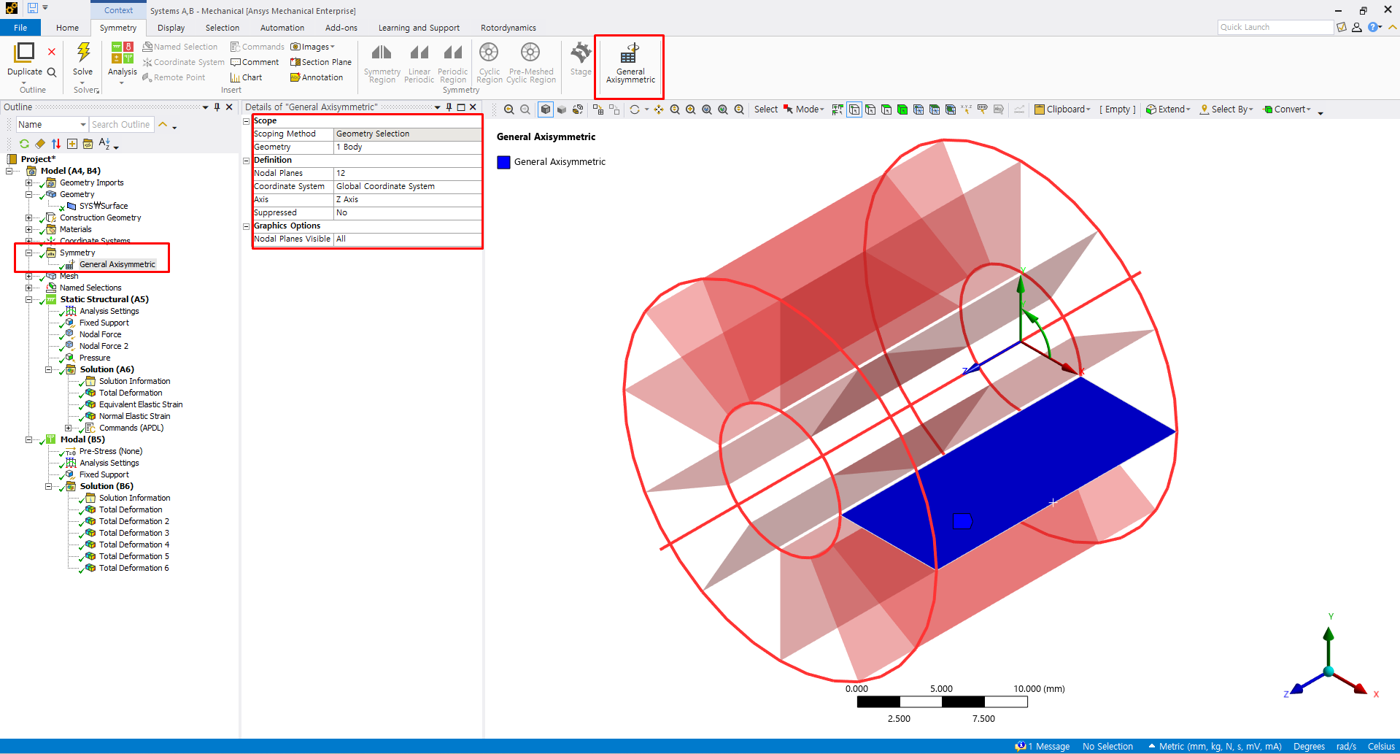
[그림 3] General Axisymmetric 설정 화면
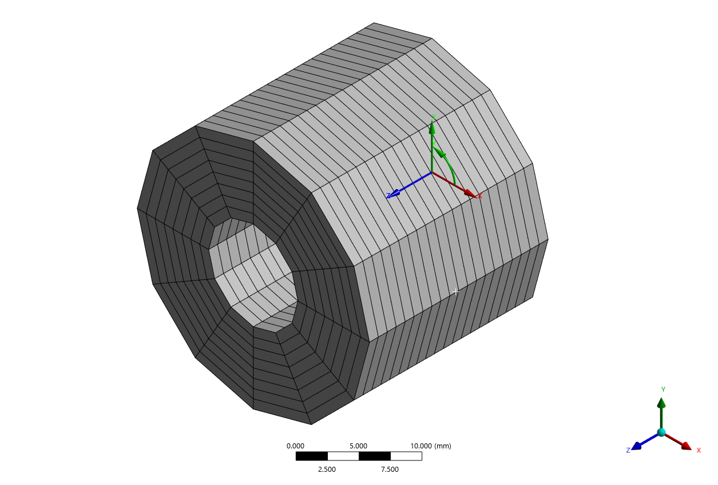 [그림 4] General Axisymmetric 요소를 이용한 3차원 격자 생성 결과
[그림 4] General Axisymmetric 요소를 이용한 3차원 격자 생성 결과
■ 해석 조건 설정
[그림 5]와 같이 단면의 특정 Edge를 선택하여 일반적인 Fixed Support를 적용할 수 있다. 단면 기반으로 입력한 구속 조건은 θ 방향으로 확장된 전체 요소에 동일하게 반영된다.
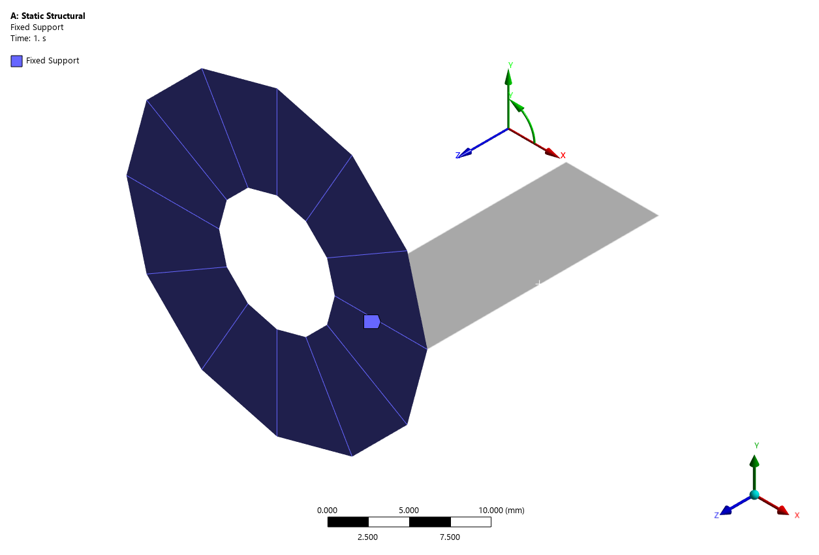 [그림 5] 축대칭 단면 Edge에 적용된 Fixed Support
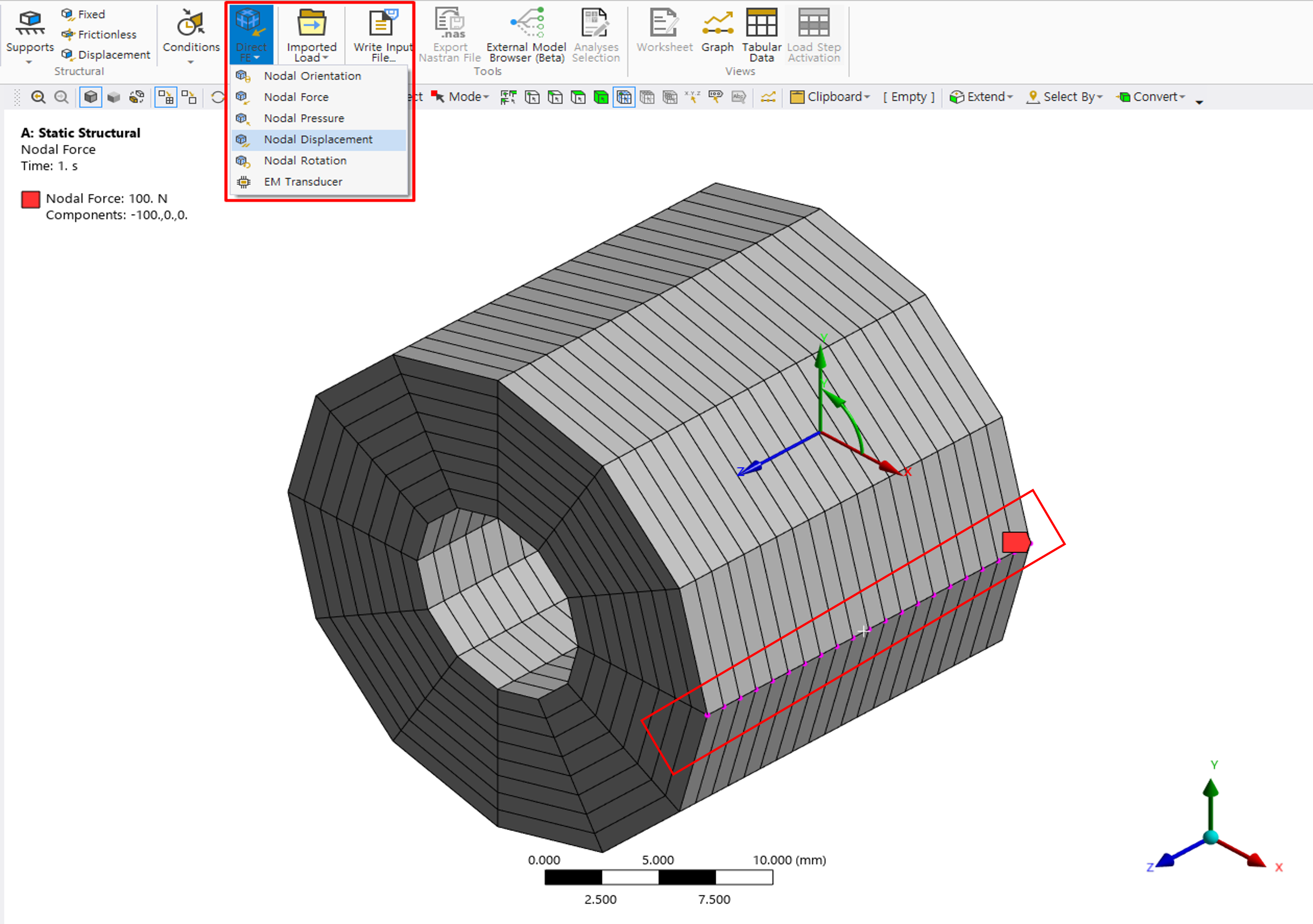
[그림 5] 축대칭 단면 Edge에 적용된 Fixed Support비대칭 하중이나 편심 조건과 같이 Geometry 기반 입력만으로는 표현이 어려운 하중 조건은 Direct FE 방식을 사용하여 Node 단위로 하중 또는 구속 조건을 지정할 수 있다. [그림 6]은 특정 Node에 하중을 직접 입력하는 예를 나타낸 것이다.
■ 해석 결과
[그림 7]은 전체 변형 및 응력 분포 결과를 나타내며, 원주 방향으로 균일하지 않은 하중 조건이 구조 응답에 그대로 반영된 것을 확인할 수 있다. 이는 단면 기반 모델임에도 실제 3차원 구조 거동을 효과적으로 재현할 수 있음을 보여준다.
[그림 7] 변형 및 응력 결과
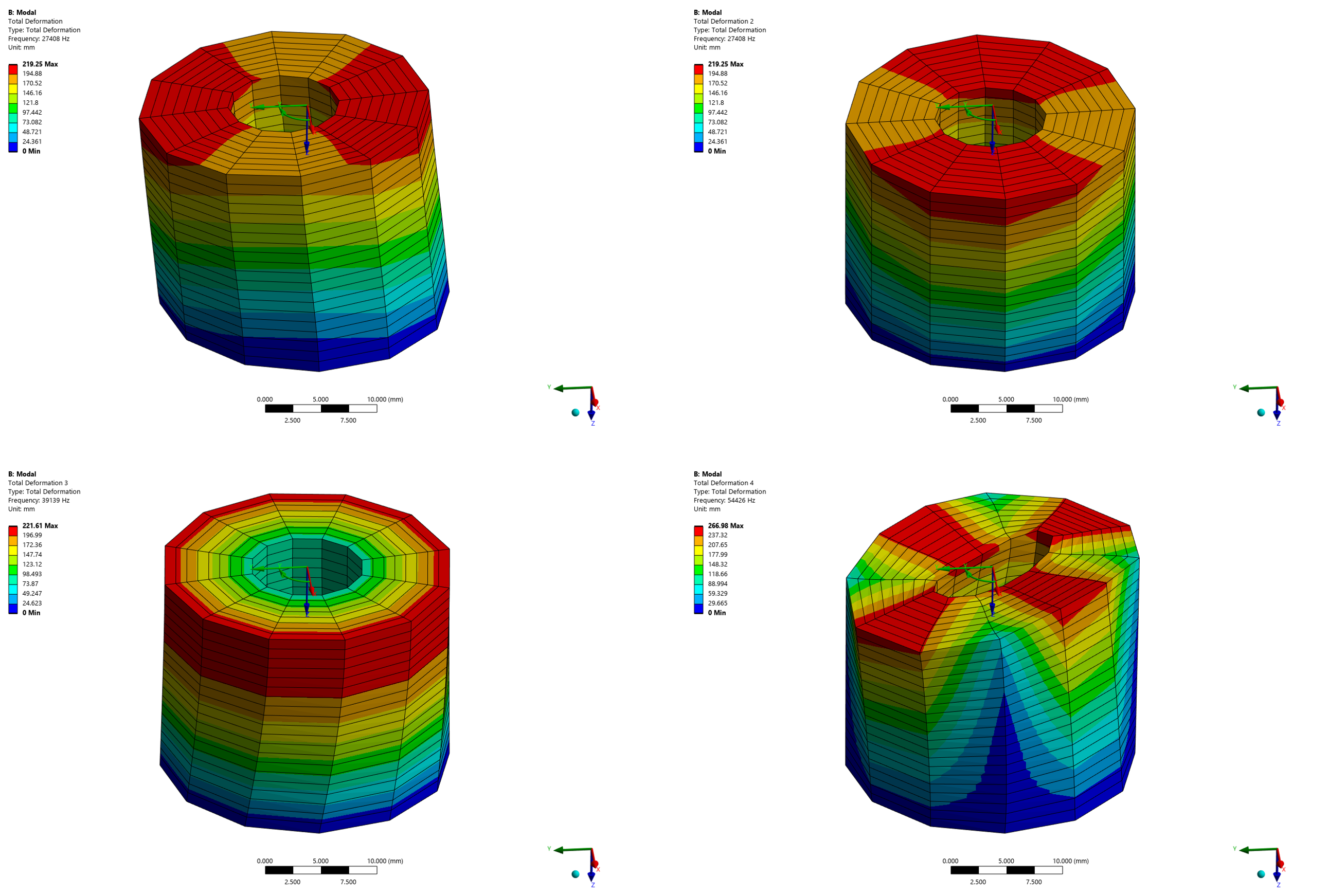
[그림 8] General Axisymmetric을 적용한 모드 해석 결과 (1~4차 모드)
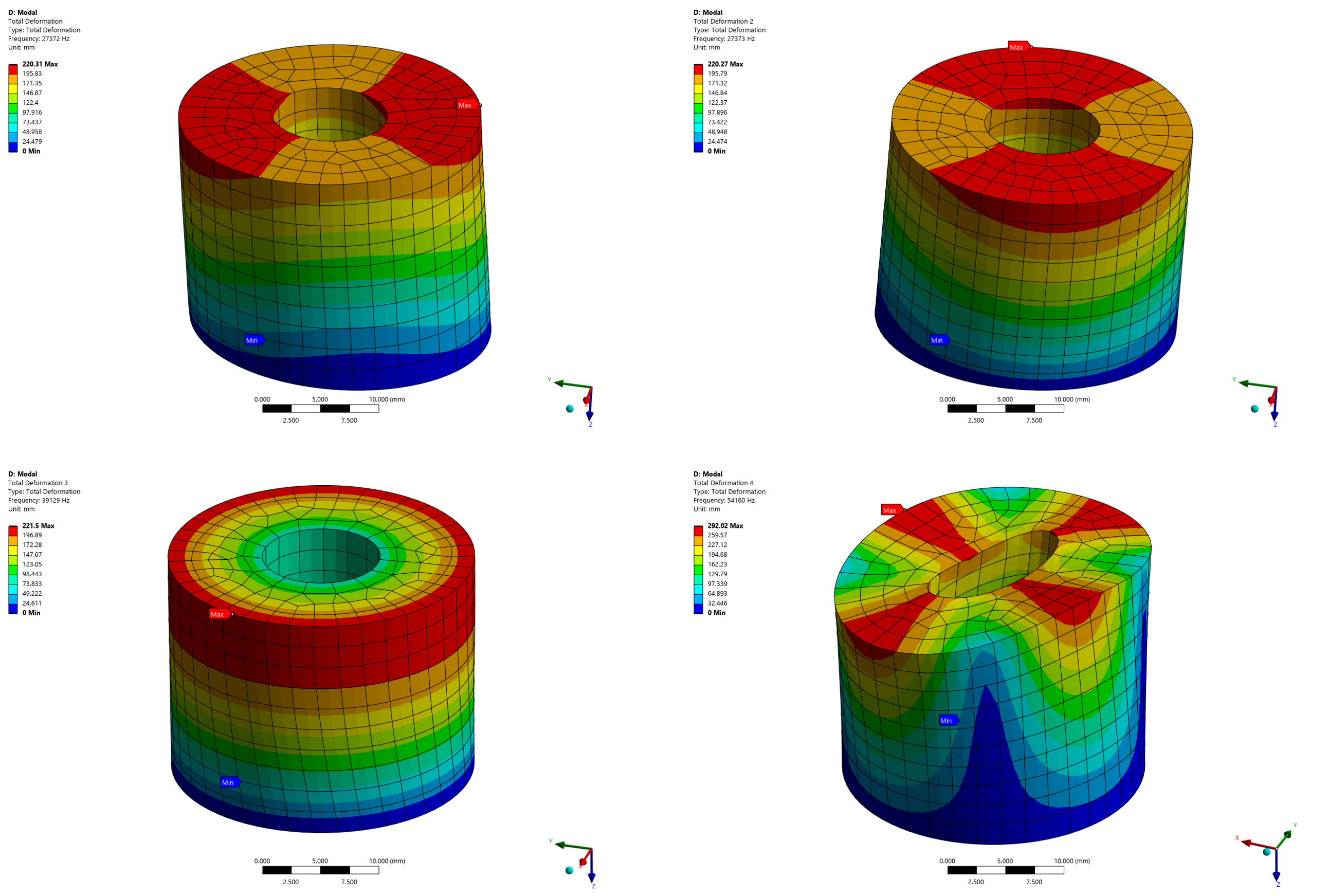
[그림 9] Full 3D 모델의 모드 해석 결과 (1~4차 모드)
맺음말
본 고에서는 축대칭 구조의 비대칭 거동을 효율적으로 해석할 수 있는 General Axisymmetric 요소의 활용 방법을 살펴보았다. 단면 기반 모델링만으로도 3차원 구조 거동을 빠르고 직관적으로 분석할 수 있어 다양한 산업 분야에서 활용성이 높을 것으로 기대된다.







 ㈜태성에스엔이
㈜태성에스엔이